The first part of this article presented secure hash algorithms, the basic building blocks for password hashing. This part will now show how to apply these building blocks to construct a reasonable password hashing algorithm.
Take it with a Pinch of Salt
Since we now know much more about secure hash functions, can we use something like SHA-256 or maybe better SHADBL-256 or SHA-512/256 to hash our password and go on to solve other problems? … Well, yes, you could, if you happen to be in the lucky position of having only users who choose perfect (randomly generated and reasonably long) passwords.
Chances are that your users are not like that. So finding a users password from an SHA-256 hash like c1b6c828073584783df115d121c04b760393dec69593ebf02b1e7c7cf4f03703 might be as easy as asking Google:
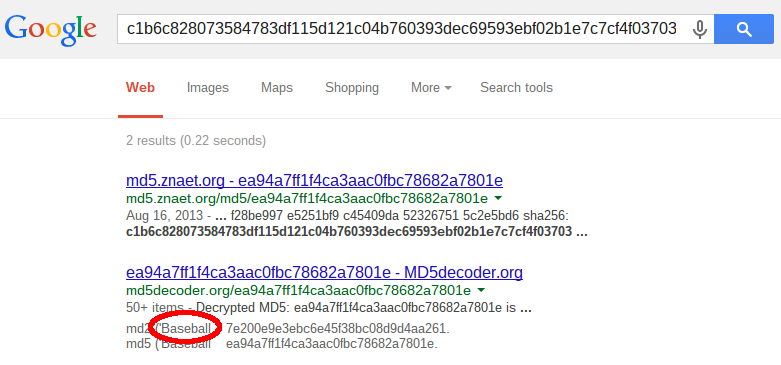
And really, the value happens to be the SHA-256 hash of Baseball (in ASCII), which, by the way, is one of the most often used passwords.
I have to admit, it is really, really difficult to protect users which choose passwords ranking in the top 10 of the most often used passwords such as Baseball. On the other hand using SHADBL-256 or SHA-512/256 instead of plain SHA-256 might already thwart this “Google attack”. (I admit I did not check and will leave that as an exercise for the interested reader.)
But for a skilled attacker plain secure hashes will always be relatively easy to crack. If, for example, you have a 100’000 stolen password hashes from some online service, you only need to execute a single hash operation before checking for 100’000 possible matches with a simple database search. And you can easily precompile tables of hashes offline long before actual attacks (possibly in the form of rainbow tables) or even just download such tables from the Internet, further speeding up your attack by trading processing time against storage space (which is very cheap nowadays). Add modern forms of dictionary attacks (which also breaks seemingly “good” passwords like poIU09*&l1nk3d1n) a plain hash offers no significant difficulty for an attacker.
It is a pity that so many systems still use simple hashes to “protect” their passwords, because the defense against the “multiplication effect” when attacking large databases and all precomputation attacks like rainbow tables is very simple: you just have to add a crucial ingredient called salt.
A cryptographical salt is a random value which is added to the password before hashing to make every password hash randomly unique no matter what the actual password may be. Using such a random salt we can spice up our plain hash of, say, SHADBL-256:
KDF(P, S) := { S, H := SHADBL-256(P ∥ S) }
where P is the password and S, the salt, is a random sequence of bytes generated by a cryptographic random number generator (RNG). Note that for each password hash a new random salt is generated. The output of the KDF now is a pair of two values, the generated salt S and the calculated hash value H.
When the user sets his password, the application will generate a new salt calculate the hash value H and store the pair { S, H } in the database. Note that the salt does not need to be kept secret and will be stored together with the hash value in the password entry. When the password needs to be validated, the application will retrieve the password entry of the specified user and recalculate the hash value H’ from the stored salt S and the password entered to login. If H’ matches the stored hash value H the user entered the correct password.
We also need to decide on the size of the salt. In literature (especially older ones) you will often see salt values of 64 or even just 32 bits (conveniently a long on many platforms). But generating some (pseudo) random bits with an appropriately seeded pseudo random number generator (PRNG) and hashing these is rather cheap, and also storing a few additional bytes of salt along with the password hash should be no issue on most systems. So there is no good justification to make the salt smaller than the final hash value. On the other hand it seems like overkill to make it bigger, so my recommendation would be to use salt values of the same size like the stored hash values, which will typicaly be 256 bits (or 32 bytes).
What do we get from the salt? Well, now the attacker cannot calculate a single hash value anymore and check it against 100’000 password hashes. Every password hash will have its own distinct salt value, forcing the attacker to calculate 100’000 password hashes to check a single potential password against all password entries. It is now also impossible to precalculate tables of password hashes, because with a 32 byte salt one would need to calculate and store 2256 different hashes for every single hashed password (one for each possible salt value).
To reasonably protect our hashed passwords against skilled attackers, we come to the following conclusion:
Always add a random salt value of at least 32 bytes when generating password hashes.
Stick to Standards
The KDF presented in the previous section is actually a quite reasonable password hashing algorithm, which you could use in practice for basic protection of stored passwords. However, in cryptography it normally pays off to stick to well known, publicly reviewed standards. It is fiendishly difficult to design secure cryptographic algorithms and protocols. Public standards have usually been reviewed and analyzed by a number of experts in the area. By using these standards instead of inventing your own algorithms you will get a lot of expertise for free and the chances that your cryptography holds up against attacks will improve a lot.
Equally important: For standard algorithms and protocols you will seldom need to write your own implementations. For most languages there are widely used libraries providing well tested implementations of the commonly used cryptographic building blocks. This not only saves you from a lot of fiddly work, it also greatly reduces the danger of implementation bugs in your cryptographic engines.
As a final welcome side effect you can also protect yourself as a developer if you stick with the standards. Should your custom protocol or algorithm be broken, you as the designer will be personally responsible for the failure. If a standard algorithm is broken, you can always reasonably argue that you just used the commonly accepted state-of-the-art solution for the problem, recommended by experts all around the world. No one will be able to hold you responsible for just following the experts advice.
So, is there a standard algorithm which we can use to generate our salted password hashes? In fact, there is one which is very similar to the KDF we defined in the previous section: the hash based message authentication code specified as HMAC in RFC 2104. The definition of the HMAC algorithm is quite simple:
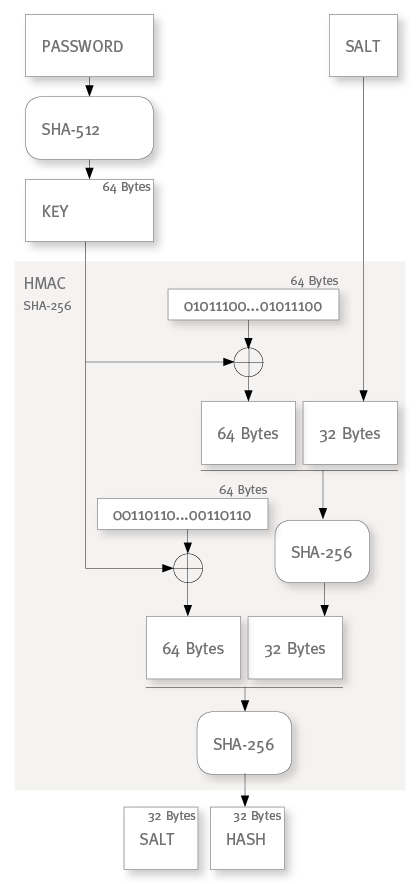
HMACH(K, M) := H( (K ⊕ opad) ∥ H( (K ⊕ ipad) ∥ M ) )
where H is a secure hash algorithm with an internal block size of B bytes, K is a secret key of B bytes and ipad and opad are fixed byte sequences built by repeating the byte 0×36 for ipad resp. 0x5c for opad B times.
True to its name, HMAC algorithms are used as message authentication codes, but they are equally suitable to produce salted password hashes if you derive K from the users password and use the generated salt as the message:
KDFH(P, S) := { S, H := HMACH(H(P), S) }
For the hash function we will typically use SHA-256 or SHA-512 (or the corresponding SHA-3 variants) which have an internal block size of twice their hash lengths. (That is, 64 bytes for SHA-256 and 128 bytes for SHA-512). In this case, if we use the same hash algorithm to derive the (fixed size) key from the (arbitrary length) password, the derived key will be smaller than the internal block size. But according to the HMAC specification we can simply pad the key with zeroes to a size of B bytes in such a case. Just make sure that your key is not smaller than the final hash value, because for smaller keys you will loose some security!
If you compare HMACSHA-256 with our KDF defined in the section above, you might see the similarities: we doubly hash the key (which essentially contains the password “normalized” to a fixed size) and also concatenate the salt into the hashed value. There are some differences as well, namely the salt is not repeated for the outer hash and the key is xored with the ipad and opad constants. The former is a tribute to the intended use case as a MAC where you want to be able to process a streamed, unbuffered message of arbitrary length. For our salted password hashing I would actually prefer to concatenate the salt a second time into the outer hash, but since I want to stick with the HMAC standard I can accept this tiny flaw. (It is highly unlikely that there will will ever be an attack depending on this theoretical little weakness, if it is one at all.)
When it comes to the ipad and opad constants I’m at a loss. Maybe some time I come around to do some research into the considerations behind these values. Until then I can only assume that someone really had a smart reason to introduce these xor operations. (Though, frankly, I have a secret suspicion that they might be just “cryptographic vodoo” to make the algorithm look more sophisticated.) In any case I don’t expect the xoring to actually reduce the security of HMAC in any way, so I’m fine with this little embellishment.
The most conventional application of HMAC for password hashing will use SHA-256 for the HMAC hash algorithm because the resulting 32 byte hash value will be an adequate size for a password hash value. In that case you could also use SHA-512 to derive the key which nicely matches with the 64 bytes internal block size of SHA-256:
Expensive is Sexy
While HMACSHA-256 as shown above is certainly reasonable for our password hashing, we should ask ourselves why not to use HMACSHA-512 instead. The typical reason to prefer SHA-256 over SHA-512 is the better performance of SHA-256. But, as I will explain in the next part of this article, we are in a rather unfamiliar situation when hashing passwords: we actually want to choose expensive algorithms because this will make the attackers life more difficult.
Given that we intend to make our password hashing as expensive as possible, I would actually recommend to prefer HMACSHA-512 over HMACSHA-256:
KDF(P, S) := { S, H := HMACSHA-512(SHA-512(P), S) }
Since SHA-512 has twice the hash size of SHA-256 you might also double the salt size for this KDF variant and store 128 bytes per password entry (a 64 byte salt and a 64 byte hash). But such sizes are most probably overkill, so I would recommend, to normally use a salt of 32 bytes and truncate the output of the HMACSHA-512 to 32 bytes as well.
If your crypto library happens to support HMACSHADBL-512, HMACSHAD-512 or HMACSHA-512/256 there is nothing wrong in using any one of these:
KDF(P, S) := { S, H := HMACSHADBL-512(SHA-512(P), S) }
And, last but not least, to future proof your application you might also opt to use HMACSHA-3 (where I would recommend a hash size of 256 bits).
In the end it will not be very important which of the secure hash functions you use as long as your salt and final (possibly truncated) hash value have a size of 32 bytes. (You could use sizes bigger than 32 bytes, but I would not expect much additional security from 48 or even 64 byte hash or salt sizes.)
Room for Improvement
Using salt and HMAC we have been able to construct a really reasonable KDF for password hashing (which, by the way, is also perfectly suitable for key derivation). But in the last section I claimed that making our algorithm expensive would strengthen it against attacks. This statement might need some explanation.
And assuming it were true, shouldn’t we be able to construct even much more “expensive” algorithms? The third part of this article will go into the details of making password hashing more expensive (and explain why we would want to do this) and present the modern password hashing algorithms PBKDF2 and scrypt.
